实验背景

资产价格预测是金融学类各专业的重要教学内容，而如何运用金融大数据与机器学习方法，从众多指标中提取真正能够解释与预测资产价格的有效指标正成为近几年金融市场研究的热点。将最新的学科研究成果转化为教学内容、并通过基于机器学习的课程实验予以验证，对学生创新精神和实践能力的培养尤为重要。

目前有机器学习功能的资产定价商用系统存在实盘交易中，不仅价格奇高、实验功能受限，而且实验的失败率也高，学生无法体验和验证自己的创造性思维，也无法多次尝试与错误修正。通过运用多种机器学习方法的虚拟仿真实验，解决了实验时间、场地受限问题，学生可以自主反复练习；学生可以体验和验证自己的创造性思维，挑战实验的广度和深度，训练初步科研的思想，提升了实践能力和创新能力；通过多次尝试与错误修正，可以有效训练学生的实验技能，提高未来实盘交易的成功率，实现虚实互补。

基于机器学习的资产定价虚拟仿真实验依托于核心课程，课程实验分成传统实验和虚拟仿真实验两个部分：利用实时行情建模分析等内容通过传统实验进行，运用机器学习算法提取有效指标等内容通过虚拟仿真实验进行，实现虚拟仿真实验与传统实验相结合，充分体现“虚实结合、能实不虚”的特点。

实验目的

资产价格预测是金融学类各专业的重要教学内容，而如何运用金融大数据与机器学习方法，从众多指标中提取真正能够解释与预测资产价格的有效指标正成为近几年金融市场研究的热点。将最新的学科研究成果转化为教学内容、并通过基于机器学习的课程实验予以验证，对学生创新精神和实践能力的培养尤为重要。

目前有机器学习功能的资产定价商用系统存在实盘交易中，不仅价格奇高、实验功能受限，而且实验的失败率也高，学生无法体验和验证自己的创造性思维，也无法多次尝试与错误修正。通过运用多种机器学习方法的虚拟仿真实验，解决了实验时间、场地受限问题，学生可以自主反复练习；学生可以体验和验证自己的创造性思维，挑战实验的广度和深度，训练初步科研的思想，提升了实践能力和创新能力；通过多次尝试与错误修正，可以有效训练学生的实验技能，提高未来实盘交易的成功率，实现虚实互补。

基于机器学习的资产定价虚拟仿真实验依托于核心课程，课程实验分成传统实验和虚拟仿真实验两个部分：利用实时行情建模分析等内容通过传统实验进行，运用机器学习算法提取有效指标等内容通过虚拟仿真实验进行，实现虚拟仿真实验与传统实验相结合，充分体现“虚实结合、能实不虚”的特点。

本虚拟仿真实验的主要目的：

1.掌握资产定价原理和金融数据统计分析工具，并通过实验对资产定价原理进行验证；

2.了解决定金融资产价格的公司特征因子，并掌握从金融大数据中找寻有效信息、进行资产价格预测的基本思路；

3.了解机器学习方法，并熟悉不同算法在提取金融信息时的差异；

4.掌握探究性学习的基本方法和思路。

实验原理

实验项目包括投资组合分析和数据可视化两个原理，如下图所示：

图1 实验原理结构图

1、资产定价中的投资组合分析原理

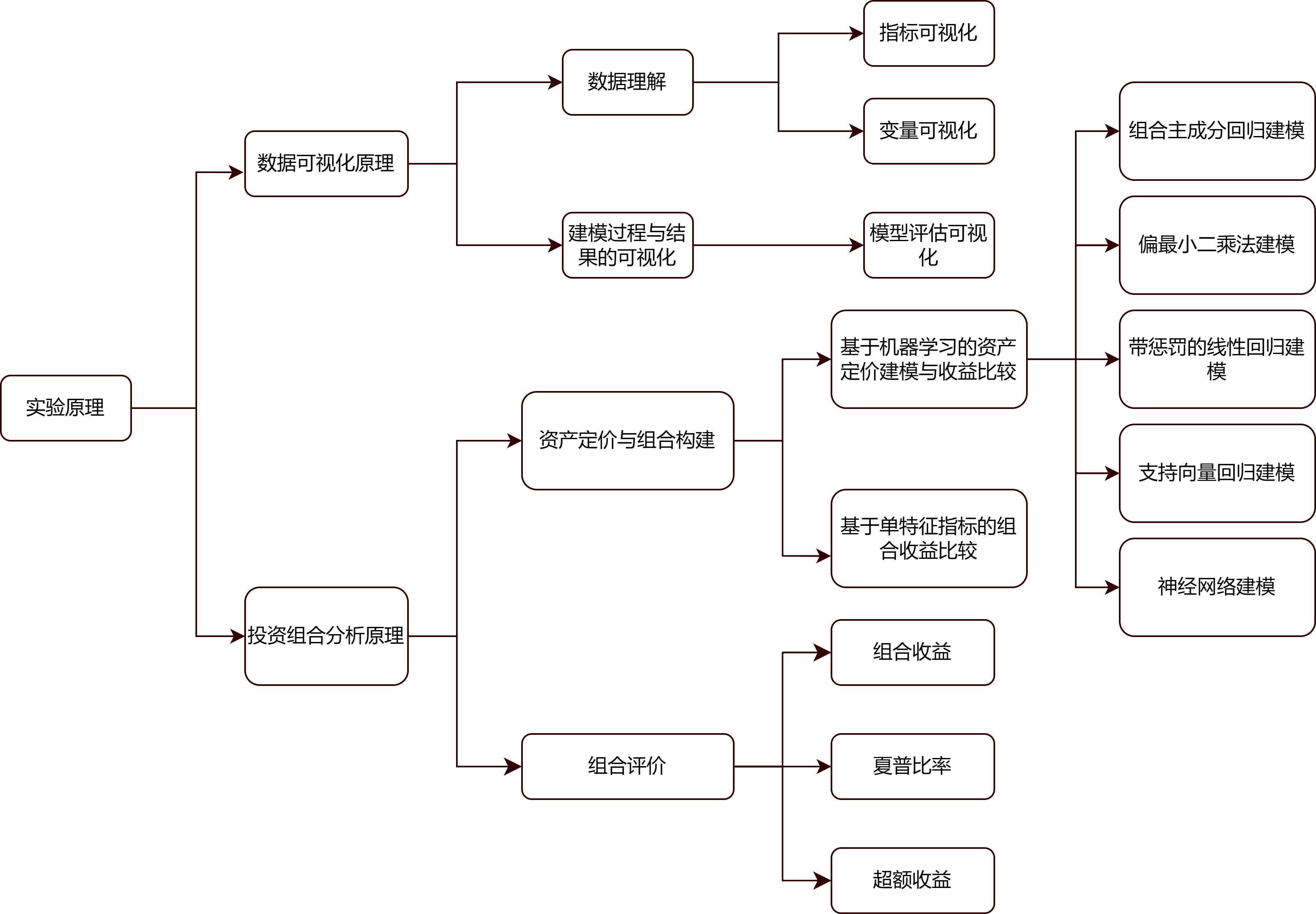
投资组合分析法是实证资产定价领域被广泛使用的分析方法。该方法在横截面股票收益预测的研究中最为常见。投资组合分析法的实质内容是：先按不同指标对股票进行排序和分组，构建投资组合并持有一定的时期；再在计算投资组合收益的基础上，比较不同投资组合的收益及超额收益是否有显著差异，从而检验不同指标对于横截面股票收益是否产生影响。实验项目中使用的投资组合分析方法，具体而言，是在每个月的第一个交易日，分别根据上个月公司最新的特征变量进行收益预测，按照预测值的大小从小到大对样本中全体公司进行排序，等分为10组，各组分别构造组合，并构造多空对冲组合。这些组合的持有周期为一个月。到了下个月，重复上述过程构建和持有新的组合。如果最终多空对冲组合能够产生显著收益，则证明使用不同的方法进行排序的预测收益指标能够显著预测横截面股票收益。项目使用的机器学习方法是在个股层面利用公司特征与行业均值共 60 个变量进行训练，最终对未来一期的公司股票收益进行预测。我们分别构造市值加权组合和等权组合，重复上述实验，对结果进行比较。同时，采用计算组合收益（等值加权、市值加权）、夏普比率、超额收益等组合评价方法，比较各组合与市场组合（以市场指数代替）的优劣，以确定不同的方法是否能区分和预测横截面股票收益。

2、数据可视化原理

数据可视化是理解数据的内涵、寻找数据蕴藏规律的一种重要手段，同时也是大数据分析的一个重要研究方向。它是资产定价研究和应用的新趋势，是实验项目的重要一环。

数据可视化，既有前期的数据理解，又有后期的建模过程与结果的可视化。采用多种统计图表对每个变量或多个变量进行可视化，或者按照行业、市场等分层对公司数据的综合指标数据进行可视化，有助于对数据的理解，为后续的变量筛选、变形及建模提供基础性信息；建模过程与结果的可视化有助于调整参数和模型评估。

实验步骤

学生通过网络进入虚拟仿真系统，了解实验项目和要求，预先补全所需前期知识。

1. 教师在线上“理论知识”模块共享实验教学的目的、原理、操作步骤、理论背景与评分标准。

2. 学生可通过远程学习方式熟悉实验教学过程，并完成实验教学预习内容、参加预习考核。

3. 学生实验分组，一个教学班可分成若干组，每组 4 人，通过抽签、两两配对。根据选定的实验，分组讨论各投资策略中指标与算法的选择，提交《数据分析及投资策略计划书》。

4. 教师设定机器学习运算训练集的实验场景及投资组合的调整时点。

5. 学生开展探究式学习，透过可视化查看和理解公司特征，选用不同的机器学习方法，不断调整变量集合和机器学习方法的参数，选择最优的变量集、方法和相关参数结果，并通过样本外预测不断调整公司特征的预测权重以及投资组合中的股票权重，整理数据结果并撰写实验报告与报告展示。

6. 完成实验后，学生可在系统“问答专区”模块针对仿真实验某些环节与老师、同学进行进一步讨论，巩固实验知识点，对实验教学项目设计进行反馈，实现真实与虚拟环境互动。

资产定价建模

1、基于单特征指标的投资组合收益计算与比较

将公司股票按照人工选择出来的某个最重要指标进行排序、分组，计算投资组合收益，记录该重要指标的变化。

2、组合收益主成分回归建模

第一步，使用主成分分析法依次提取各公司特征的最大方差部分。

假设资产收益与公司特征之间存在线性关系：

R = (X δ_{K}) α_{K} + E

(1)

其中，𝑅代表𝑁𝑇 × 1阶由预期收益组成的矩阵，𝑋为𝑁𝑇 × 𝐶阶由公司特征组成的矩阵（𝐶为140个公司特征变量），𝛿𝐾为𝐶 × 𝐾阶系数矩阵，𝛼𝐾为𝐾 × 1阶系数矩阵。式中，𝑋𝛿𝐾表示经过数据降维后新生成的𝐾个预测因子，即将数据从𝐶个公司特征变量降维到𝐾个指标。

第二步，进行主成分回归，用交叉验证确定最终进行预测回归的主成分数量。

第三步，计算预测回归结果。

3、带惩罚的线性回归建模

当使用的预测变量较多时，简单的回归分析容易产生过度拟合的问题。带惩罚的线性回归通过在回归最小化的损失函数中加入惩罚项，“牺牲”一部分参数估计的无偏性，从而对变量进行适当地选择和赋权。其目标方程可以写为（2）的形式：

L (β; \cdot) = \frac{1}{N T} \sum_{i = 1}^{N} \sum_{t = 1}^{N} (R_{t + 1} - f (X_{i, t}; β))^{2} + ϕ (β; \cdot)

(2)

其中，

𝑅_{𝑡 + 1}

是预期收益，

𝑋_{𝑖 𝑡}

是第 i 个公司特征，𝛽是系数矩阵，𝑓(

𝑋_{𝑖, 𝑡}

;𝛽)是由公司特征组成的线性预测方程，𝜙(𝛽;∙)是不同的惩罚方程（Penalty function）。当惩罚方程的具体形式依次采用（3）至（5）式，即是岭回归（Ridge regression）、套索回归（LASSO regression）、弹性网络（Elastic net）三种方法：

ϕ (β; λ)_{R i d g e} = λ \sum_{j = 1}^{N} β_{j}^{2}

(3)

ϕ (β; λ)_{L A S S O} = λ \sum_{j = 1}^{N} | β_{j} |

(4)

ϕ (β; λ, α)_{E l a s t i c N e t} = \sum_{j = 1}^{N} λ (α | β_{j} | + (1 - α) β_{j}^{2}

(5)

其中， $𝛽_{j}$ 为第 j 个公司特征的系数，𝜆为控制着惩罚方程在目标方程中的所占比重。当𝜆越大时，变量受到的惩罚方程压缩的程度会更深。惩罚方程中𝜆与𝛼的都属于超参数，是在回归前由训练集上交叉验证来确定的。

4、随机森林建模

前两种方法都是基于线性模型的假设进行预测。在实际应用中，公司特征与资产收益的关系往往是非线性的，因此，项目实验使用了一种新的非线性方法——随机森林回归。

随机森林模型在基学习器训练中引入了随机属性，传统树模型在进行分支时考虑在当前节点的属性集合选择一个最优、损失率最低的属性。而在该模型中，基学习器的属性集合为总集合的一个子集，即在子集中选择最优属性来进行划分。

5、神经网络建模

目前，神经网络方法在金融预测研究中逐渐被推广。项目实验使用“前馈”（Feed-forward）神经网络，隐藏层从一到三层，如图2所示。

图2 神经网络法的运算结构

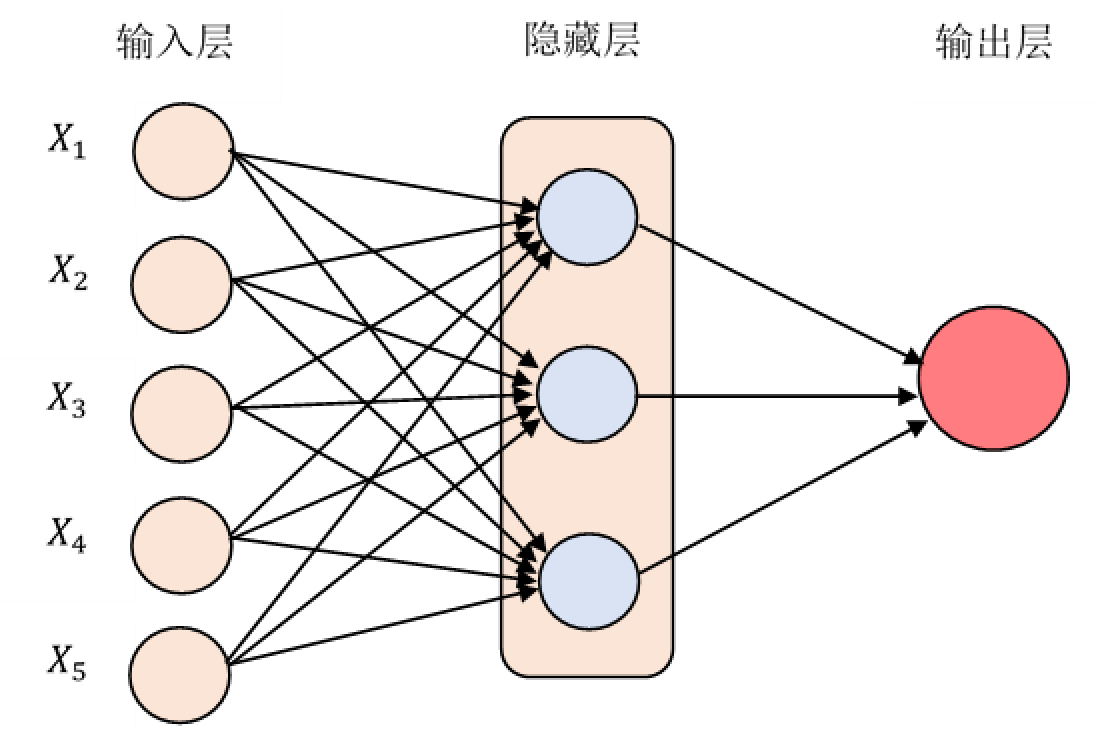
对于不同层数的节点数，我们可以在试验系统中进行选择，如2到32个节点。当数据样本较小时，运用神经网络模型并不是层数越多预测结果越好；同时，由于金融市场本身各类指标包含不同噪音，因此，当模型层数越多时很可能会放大这类噪音对结果的影响。由于使用交叉验证法确定神经网络模型层数和神经元数量的运算量太大，因此进行了一定程度的简化。最后，项目实验使用了多重随机种子对神经网络模型进行初始化、构建公司特征间的关系，并对不同模型的预测取了平均值。目的是既减少了预测收益的方差，又能更好地通过大量随机实验的方式对模型预测结果进行优化。

组合评价

1、组合收益

组合收益主要包含用等值加权法和市值加权法构造投资组合，并计算每个投资组合的收益。其中，等值加权法的核心思想就是对投资组合中的每只股票投入的权重相同。因此，用该方法构造的投资组合收益为每只股票收益的算术平均值，具体算法如下式所示。

R_{e p, t} = \frac{\sum_{i = 1}^{n} R_{i, t}}{n}

(1)

上式中的

𝑅_{e p, t}

表示等值加权法构造的投资组合（Equal weighted portfolios）在t期的收益率，

𝑅_{i, t}

为公司i在t期的股票收益率，n为投资组合中股票的数目。

市值加权法则根据公司t-1期的流通市值

𝑀 𝑉_{𝑖, 𝑡 - 1}

与所有公司的总流通市值之比来决定每只股票的投资权重，并在第t期用个股真实收益乘以投资权重计算投资组合真实收益。用该方法可以避免在规模较小的公司中投入过多资金从而造成其价格的波动。

2、夏普比率

夏普比率反映投资组合每单位风险的收益补偿。夏普指数越高，组合越理想。夏普比率的定义式为

S_{p o r t} = \frac{E (R_{p o r t}) - R_{f}}{σ (R_{p o r t})}

(2)

其中， $S_{p o r t}$ 为夏普比率； $E (R_{p o r t})$ 为组合预期收益； $R_{f}$ 为无风险收益，这里用一年期国债利率代替； $σ_{p o r t}$ 为组合的标准差，反应组合的总体风险大小。

3、超额收益

投资组合所获得的超额收益是指通过对不同的资产定价模型所包含的定价因子进行回归分析时，得到的回归方程截距项大小。统计意义上显著的超额收益意味着该投资组合包含着不能被定价因子所解释的信息，往往对补充和优化现有的定价模型有着较大意义。项目使用资本资产定价模型（Capital asset pricing model, CAPM）、Fama and French三因子模型和五因子模型来衡量投资组合超额收益的大小。

首先，对于使用CAPM模型进行回归，其回归方程如式（3）所示。

R_{i, t} - R_{f t} = α_{i, t} + β_{M K T} (R_{M K T, t} - R_{f t}) + ε_{i, t}

(3)

上式中，由CAPM模型衡量的超额收益是进行多因子回归后的截距项大小。回归方程的被解释变量是各投资组合的收益与无风险收益（一年期国债收益率）之差，解释变量是理论中提出的定价因子。超额收益也被称为风险调整收益（Risk-adjusted returns），如果CAPM模型中衡量系统性风险的市场因子能够完全解释投资组合收益，则超额收益α应该趋于0且不显著。超额收益越大越显著体现出投资组合溢价水平越高，意味着由某个指标所构建的投资组合市场异象程度越深、套利空间越大。

核心要素的仿真度

项目的核心要素包括基础数据、机器学习方法以及数据可视化。

1. 基础数据的仿真度

基础数据采用真实历史数据。从理论上说，资产定价是通过对市场及公司财务的未来表现做出准确预期，在此基础上，运用某种定价模型对公司投资价值进行估算。由于准确预期市场及公司未来资产价格极其困难，而历史数据则较易获取，考虑到项目是为了帮助学生掌握资产定价原理，理解公司特征因子对资产价格的决定作用。因此项目直接采用历史数据代替预期数据，这不仅保证了数据的客观性和真实性，而且也简化了实验过程，突出了实验重点。实验项目主要使用了真实的历史财务数据和股票交易数据作为学生进行实验的材料，这一比一地还原了资本市场的历史特征，也使得学生能够更直观地将投资策略与历史真实事件进行逐一对比。这反映了实验极高的仿真程度。

2. 机器学习方法的仿真度

使用机器学习方法仿真投资过程。采用信息技术，利用历史数据开展机器学习，仿真投资者的思维和学习过程，通过不断优化算法，以求得最佳结果。其好处是运用大数据思维，排除人的主观局限性和预设模型的局限性，以保证运算过程的客观性、科学性和准确性。

学生在实验中使用机器学习方法进行资产价格预测时，需要不断试错以得到最优的预测结果。这一过程模拟、仿真了投资实践中对资产价格变动成因的挖掘过程，具有一定的难度。同时，分组对抗的设置让学生在挑战中模拟现实不同基金的业绩比拼，将实验赋予一定的竞赛特征，使得学生更有动力去提升资产价格的预测效率。

3. 数据可视化的仿真度

数据可视化助力学生进一步分析企业特征与资产收益之间的关系。项目的仿真模拟部分还通过立体直方图直观地展现了公司特征、行业特征与股票收益之间的关系。学生可以通过数据可视化的分析，结合后续的机器学习方法，进一步了解公司特征与资产收益的关系。项目通过虚实结合地方式，将这一抽象过程进行了还原，引导和启发学生思考。